Os voy anticipando que veremos:
1) Problemas de Álgebra:
EDADES:
Como este problema son:
a) Ana es 7 años mayor que Pedro y 5 menor que Pablo. Sabiendo que hace dos años sus edades sumaban tres siglos, una década y un lustro, ¿qué edad tienen todos actualmente?
b) Alejandro es 5 años mayor que Alonso y 2 menor que Pilar. Si el año pasado sus edades sumaban un siglo, ¿qué edad tienen todos actualmente? (Ayuda: no da exacto, pero debes interpretar las edades como se hace oficialmente. Aunque tengas 12 años y medio, en Matemáticas 12,5, no se considera que tienes 13 hasta el día de tu cumpleaños).
c) Un padre duplica la edad a sus mellizos y dentro de una década sus edades sumarán cuatro siglos. Calcula la edad de todos actualmente. ¿Es esta situación posible? (Ayuda: contesta a la última pregunta cuando resuelvas el problema, con los resultados en la mano).
Os subo una imagen de este problema resuelto por otra de mis alumnas extraordinarias:
IGUALAR CANTIDADES:
Como este problema son:
a) Juan tiene el triple de canicas que Pilar. Después de unas cuantas partidas, Juan pierde 5 canicas y entonces, su número de canicas solo supera en 8 al de Pilar. ¿Cuántas canicas tienen ambos amigos después de todos estos juegos?
Así enunciado, da un resultado decimal, que no tiene sentido al tratarse de canicas, como me ha comentado una alumna, que me ha mandado esta maravilla:
Por ello, os sugiero que lo resolváis con este enunciado alternativo:
Juan tiene el triple de canicas que Pilar. Después de unas cuantas partidas, Juan pierde 6 canicas y entonces, su número de canicas solo supera en 8 al de Pilar. ¿Cuántas canicas tienen ambos amigos después de todos estos juegos?
b) Antonio tiene dos docenas de cromos más que Luis y, después de comprarse 3 paquetes (10 cromos cada paquete), su número de cromos ha pasado a triplicar al de Luis.
c) En una estantería hay el triple de libros que en un sinfonier. Pero si quitamos una docena de libros de la estantería y se los pasamos al sinfonier, en ambos sitios habrá la misma cantidad de libros. ¿Cuántos son?
IGUALAR A UN DATO:
Como este problema son:
a) Un sillón vale 30 € más que una silla. Si hemos comprado 3 sillones y 5 sillas por 890 €, ¿cuánto vale cada tipo de mueble?
b) Un camión lleva naranjas y plátanos. Sabiendo que la caja de naranjas pesa medio kilo más que la de plátanos y que el camión carga, en total, 1993 Kg de fruta, repartidas entre 40 cajas de plátanos y 26 de naranjas, ¿cuánto pesa la caja de cada tipo de fruta?
c) Una blusa vale 8,55 € más que unos pantalones antes de las rebajas. En rebajas, vemos que la blusa tiene una rebaja del 25% y los pantalones solo del 10%. Si finalmente nos llevamos ambas prendas, una vez rebajadas, por 250€, ¿cuánto hemos pagado por cada una? ¿Cuánto costaban antes de las rebajas? (Ayuda: el total, que siempre se considera como el precio sin rebaja, es el 100%. Con una rebaja del 20% se paga el 80%, por ejemplo. Utiliza esta información para plantear lo que se paga por la blusa y por el pantalón después de las rebajas. Plantea una tabla con los precios antes y después de las rebajas.)
MEZCLAS:
Como este problema son:
a) Se mezclan vino tinto, a 8 €/L, con zumo de naranja, a 3,5 €/L, para hacer sangría a 5 €/L. Si se desea fabricar 32 L de esta sangría, ¿qué cantidad de cada componente hay que añadir?
b) Para hacer el café que le gusta a Pedro, hay que mezclar café natural, a 4 €/Kg, con café torrefacto, a 6,7 €/Kg, para lograr un café mezcla a 5 €/Kg. Si Pedro quiere 10 Kg de esta mezcla de cafés, ¿cuánto debe añadir de cada tipo?
c) Resuelve el problema de mezclas para fabricar natrón para un momificador, propuesto en el capítulo 11 de la novela "El Caballero de la Noche", que tienes colgada en esta misma página, a través de la Mediateca.
Mirad esta resolución tan esmerada de una alumna:
Aquí os dejo algunos ejercicios del libro, resueltos por alumnos y alumnas muy trabajadores:
En este otro, sale también muy claro el tipo de problema de "igualar a una cantidad":
Horario oficial de clases: LUNES y MIÉRCOLES a las 11:30 horas.
Mirad: antiferroelectrica o Pilar López del Castillo.
Los alumnos deberán enviar a la profesora los ejercicios encomendados en ellas para su revisión y puntuación.
2) Ecuaciones con denominadores.
3) Estudio de la obra de teatro matemático e histórico: "Matemáticas en Egipto"
Puede descargarse de:
Los alumnos tienen los capítulos 11 y 12 de la obra en fotocopias entregadas durante las clases. Si las han perdido, ellos mismos deberán imprimirlas desde el pdf que aparece aquí. En clase se les dirá qué parte deben aprender, o saldrá publicado en el blog, según el papel asignado a cada uno.
Reparto de papeles en la obra de teatro matemático e histórico (1º ESO E):
Narradores:
Daniel G. el capítulo 11
Félix C. el capítulo 12
Ramsés II:
Daniel S. (capítulo 12)
Teremun:
Omar (capítulo 11)
Embalsamador Makalani:
Jason (página 206). Solo debe decir una frase, por lo que, aprovechando el disfraz de egipcio que llevará, también hará el papel de sacerdote egipcio en el templo de Karnak (páginas 210 y 211)
Momia:
Iván
Hacker 064:
Marcelo comenzará el capítulo 11 (páginas 201 a 205) Explicará el problema de mezclas, que hará Farouk (página 205).
Jaime comenzará el capítulo 12 (páginas 215 a 219) y hará el problema de edades (página 219) para el faraón, mientras lo explica Sergio. Entonces aparecerá Daniel B. que se quedará desde la frase "Lo siento mucho" (página 219) hasta el final, donde hará el problema de fracciones final para el faraón, que también explicará Sergio. Tened en cuenta, como os dije en clase presencial, que es muy difícil ejecutar y explicar a la vez.
Visir:
Daniel H. en el capítulo 12 (páginas 216 a 220) y explicará el problema de enteros tan sencillo de la página 218, mientras lo hace. Es el problema más sencillo.
Julio hará de visir también, pero para el grupo de 1º ESO B, con quien ya estaba asociado en este trabajo.
Agentes del futuro (chicas):
Comenzarán el capítulo 11 desde la página 206: Natalia (como Musicática), Lucía (como Musicática) y Vanessa (como Captime); las tres hasta la página 210, donde Natalia ejecutará el problema de Proporcionalidad basado en la ley del respeto egipcia en el templo de Karnak. Mientras lo ejecuta, lo explicará Ruth. Esta última enunciará el teorema de Pitágoras que veremos a comienzos de la 3ª evaluación. Todas ellas terminarán el capítulo 11. En el capítulo 12, Ruth hará de Musicática, Lucía de Captime y Vanessa de Musicática. Sé que Alba estaba entre las agentes, pero deseo que haga otro papel muy importante:
Presentadora:
Alba: deberá redactar una pequeña intruducción presentando al curso, y mandarme su correo electrónico para que le envíe una sorpresa para todos, que solo ella y yo conoceremos.
Para Ainhoa de 1º ESO B, creo recordar que era la última parte del capítulo 12, pero no puedo asegurarlo, pues he dejado el papel de repartos en el centro, porque repartí los papeles antes de esta baja forzosa. A la vuelta se lo daremos fijo.
4) Los alumnos deben preparar el material de Geometría:
10 láminas cartulina DIN-A4 blancas, compás en buen estado (mina, aguja, que no cambie de abertura al hacer una circunferencia), escuadra y cartabón, regla graduada (si no lo están ya la escuadra o el cartabón, y que no sea muy grande, 30-40 cm como mucho), goma de borrar y portaminas 0,5 mm o lápiz bien afilado con sacapuntas con depósito, tres pinturas de colores bien visibles y distintos (rojo, azul y verde, por ejemplo), bolígrafos azul y rojo.
Estamos viendo: "Operaciones con ángulos"
Cálculo de complementarios, cortesía de una alumna extraordinaria:
Cuando completemos la lámina con tipos de ángulos, nuestro objetivo será ser capaces de completar la hoja de ejercicios que podéis descargar de:
https://matematicasiesoja.files.wordpress.com/2018/10/ejercicioca-de-c3a1ngulos_rectas.pdf
5) Teorema de Pitágoras:
Afirma que en cualquier triángulo rectángulo (tiene un ángulo recto, es decir, de 90º, que es una esquina, una L o como mejor lo veáis) se cumple:
Este teorema puede demostrarse construyenco dos cuadrados iguales, a los que se les quitan cuatro triángulos idénticos. Entonces, de uno quedan dos pequeños; y del otro, uno grande.
Al haberles quitado lo mismo, las áreas de lo que queda también son iguales y de ahí se demuestra.
Vamos por pasos:
a) Primero dibuja dos cuadrados iguales, por ejemplo, de lado 8 cm:
No parecen cuadrados por la aberración esférica de la cámara, pero lo son.
Después, divide cada lado en 2 y 6 cm del siguiente modo:
Colorea los triángulos, y pon datos dentro de ellos:
Ahora observa el siguiente vídeo:
Os subo las fotos de un alumno que lo ha hecho muy bien:
APLICACIONES:
a) Comprobar que un triángulo es rectángulo: si sustituyes sus tres lados en el teorema, tomando como hipotenusa el más grande de los tres, y lo cumple, el triángulo es rectángulo. En caso contrario, no lo es.
b) Calcular lados desconocidos en triángulos rectángulos.
Mira la clase:
Y haz los ejercicios de las siguientes hojas:
Si quieres comprobarlo con Geogebra, entra en:
https://www.geogebra.org/geometry
Y para prepararte para el cálculo de áreas:
https://matematicasiesoja.files.wordpress.com/2018/10/perimetros-y-areas.pdf
Para comenzar con el CUADRADO, os subo la teoría copiada de una alumna que sigue muy bien las clases:
Podéis volver a ver la clase, sobre unidades de área y cuadrado en:
Aquí os dejo el ejercicio fundamental, propuesto durante la clase anterior, resuelto por una alumna excelente:
En la siguiente hoja, podéis comenzar a practicar todas estas aplicaciones del teorema de Pitágoras, que estamos viendo en las clases online con Youtube:
https://www.matematicasonline.es/segundoeso/ejercicios/Pitagoras-cuadernillo.pdf
Os ayudará la siguiente clase:
Y los deberes encomendados en ella, hechos por un alumno estupendo, que se la perdió porque la impartí antes de tiempo...
En un hexágono, tenemos 6 triángulos equiláteros iguales. Calculando el área de uno de ellos y multiplicándola por 6, tendremos el área del hexágono:
Y, si quieres comprobar tus resultados, entra en Geogebra:
https://www.geogebra.org/geometry
Aquí tenéis el pentágono de la última clase:
6) Trabajo: "Matemáticas del Brawl Stars"
Pincha en:
https://mathsforexplorers.blogspot.com/p/combinadas-y-geometria-en-el-brawl-stars.html
6) También es bueno que cada alumno vaya haciéndose con una calculadora no programable. La usarán durante toda su vida escolar y les acompañará en todos los exámenes a partir de 4º ESO y también en las pruebas PAU. En el siguiente link tenéis las calculadoras permitidas para estas pruebas. No compréis ninguna que no cumpla estas características, porque os la podrían quitar en el examen PAU:
https://www.uam.es/UAM/01-Acceso-para-estudiantes-de-Bachillerato-y-Formacio/1242695563300.htm?language=es&pid=1242656108731&title=Acceso%20para%20estudiantes%20de%20Bachillerato%20y%20Formaci?n%20Profesional
Pinchar en: "Normas sobre el uso de calculadoras y otros instrumentos"










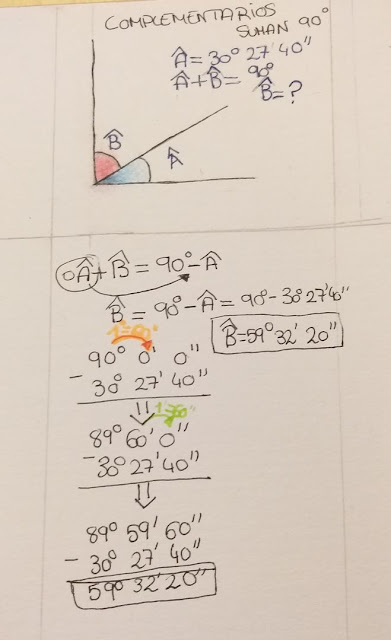


















No hay comentarios:
Publicar un comentario