Este proyecto persigue entrenar al alumnado en las múltiples aplicaciones de la materia de Matemáticas, para que sepan utilizarla como un arma de indiscutible poder irremediablemente unida al mundo de la Ciencia, los argumentos lógicos de cualquier índole, y viendo su increíble potencial, comiencen a amarla, y la aprendan:
El libro de proyecto que resume nuestro trabajo, es de nuevo una novela que se acaba de publicar bajo licencia CC-BY-SA, para que los alumnos cuenten con una guía de todas las aplicaciones matemáticas en el campo de las Ciencias, la Historia, la Lengua, y la Música especialmente. Se trata de un thriller de ficción donde:
"El protagonista Amir, un muchacho feliz con su familia, buen deportista y apasionado por la Electrónica, termina convirtiéndose en un hombre competente, que trabaja en el departamento de investigación de la gran multinacional Microbotic Systems. Sin embargo, pronto se verá obligado a investigar las razones de un horrible atentado. La reflexión que ello le supone, cambiará su vida para siempre."
Puede descargarse de:
El libro de proyecto que resume nuestro trabajo, es de nuevo una novela que se acaba de publicar bajo licencia CC-BY-SA, para que los alumnos cuenten con una guía de todas las aplicaciones matemáticas en el campo de las Ciencias, la Historia, la Lengua, y la Música especialmente. Se trata de un thriller de ficción donde:
"El protagonista Amir, un muchacho feliz con su familia, buen deportista y apasionado por la Electrónica, termina convirtiéndose en un hombre competente, que trabaja en el departamento de investigación de la gran multinacional Microbotic Systems. Sin embargo, pronto se verá obligado a investigar las razones de un horrible atentado. La reflexión que ello le supone, cambiará su vida para siempre."
Puede descargarse de:
Mostremos por tanto un breve resumen de los últimos trabajos que estamos desarrollando estos últimos dos cursos, al amparo de este trabajo, y el que trabajamos el curso pasado.
Teatro matemático en Inglés
Destinado a trabajar los temas de Proporcionalidad y Geometría, desarrolla una historia de ficción más entre la Dra. Antiferroeléctrica (la profesora de Matemáticas), y su grupo de agentes especiales "Súper-G", mientras desarrollan una entrevista en el restaurante O´Nostrum, con los mafiosos de una multinacional que pretende extender un virus mortal por el mundo, y vender el antídoto que lo cura a precios desorbitados para enriquecerse.
Nuestros agentes vigilan al cabecilla principal, y consiguen neutralizarle con ayuda del mago Arsenius, que desarrolla un extraordinario show con trucos sobre proporcionalidad con chinches venenosos ("assassin bugs"), y propone un reto de Geometría a los comensales:
Las letras de la representación teatral que aparecen en el vídeo, son trabajos de Geometría del plano, donde los alumnos han diseñado el dibujo de la letra que les tocaba, a partir de un rectángulo de las mismas dimensiones, donde inscribieron dicha letra. Después calcularon su área:
a) Por adición: sumando las áreas de los polígonos o figuras planas que formaban cada parte de la letra.
b) Por sustracción: al área del rectángulo en el que está inscrita, se le restan las áreas de los polígonos que no forman parte de la letra.
También calcularon el perímetro de la letra, resultando trabajos como los de las figuras que aparecen a continuación:
<
Puedes encontrar el capítulo que incluye esta obra de teatro en:
Teatro: "Matemáticas en Egipto"
La representación de estreno, será el día 30 de Mayo del presente curso 2019, en el salón de actos del IES Celestino Mutis de Madrid.
Pronto estará disponible el vídeo resumen con los mejores momentos de la obra, así como algunas fotos emblemáticas para el recuerdo, o la resolución de problemas de mezclas, edades y fracciones que se desarrollarán en relación con la cultura egipcia.
La introducción irá a cargo de nuestra presentadora oficial: Iciar, una de nuestras alumnas más carismáticas y organizadas, que deberá trabajar con:
Cuando termine la obra desclasificaremos todos estos archivos para que podáis utilizarlos desde otros centros, si deseáis animaros a preparar un trabajo tan productivo como este, tanto a nivel matemático, como histórico.
Energías renovables y Matemáticas
Siendo conscientes de la enorme importancia de la sostenibilidad, la primera lección con la que comienza este trabajo, es una presentación sobre la historia de la energía nuclear, resaltando aquellas personalidades de científicos importantes que contribuyeron al descubrimiento y explotación de esta fuente de energía. Conviene que los alumnos distingan los siguientes grupos:
Descubridores
Lise Meitner (doctora en Físicas)
Otto Han (doctor en Química)
Primer reactor nuclear de la historia
Enrico Fermi
Proyecto Manhatan para el desarrollo de la primera bomba atómica
Bomba H
Edward Teller
Posteriormente se comentan los riesgos para la salud de la ingente cantidad de residuos nucleares que se están generando, haciendo hincapié en el hecho de que los periodos de semidesintegración de estos materiales son de millones de años, y de que tomando las medidas oportunas, es posible autoabastecerse únicamente de energías renovables como la solar, sin tener que renunciar a nuestras necesidades energéticas. Puedes ver los resultados de esta reflexión, en la presentación que alumnos de 1º ESO y profesores vamos a representar en el IES Celestino Mutis durante la semana cultural, en una actuación por la tarde para padres, y para otros alumnos durante el período extraordinario del mes de junio:
Hemos querido acompañar la reflexión de este punto, con un proyecto de desarrollo y optimización escolar de fabricación y caracterización de células solares fotovoltaicas, utilizando materiales caseros y un procedimiento de trabajo manual sencillo y preciso, con el que hemos conseguido datos para trabajar los temas de Proporcionalidad, Porcentajes, Gráficas y Funciones:
1) Con banco óptico.
Con un banco óptico fabricado en coordinación con el departamento de Plástica: con dos cartones, un transportador y cinta adhesiva, se tiene una estructura como la de las siguientes figuras:
El banco óptico está bien orientado, cuando la sobra que proyecta el transportador es una línea.
Se puede enganchar a un trípode, si se ubica sobre un trozo de madera con un orificio para enganchar sobre el saliente del trípode.
En todos los casos se observa que dicha tensión sube hasta alcanzar un máximo, y luego comienza a bajar, dando como resultado una gráfica con forma de parábola que se abre hacia abajo, y cuyo vértice se ubica para el ángulo de apertura asociado a la incidencia perpendicular sobre la célula fotovoltaica, que es cuando desarrolla su máximo rendimiento.
A continuación mostramos las parábolas logradas con tres de los colorantes estudiados:
Y visto que el colorante más eficiente resultó ser la frambuesa, decidimos optimizar las condiciones de fabricación para este colorante.
Para estas condiciones logramos la siguiente gráfica, mejorando la tensión de respuesta, en más de un 90%:
2) En exposición directa frente al Sol
La célula se expone directamente desde la oscuridad, y se toma un vídeo de la tensión desarrollada en consecuencia hasta que llega a la saturación (valor máximo que es capaz de ofrecer). Posteriormente se cubre por completo, observando la evolución de la caída de tensión hasta que vuelve al valor de partida. Las gráficas tienen forma de escalón, con tres tramos claramente distintos:
Subida, mantenimiento y bajada.
Interpretación matemática
Los alumnos enseguida comprenden que las tres gráficas anteriores tienen tres tramos:
Por ejemplo, considérense las rectas de las siguientes figuras, con el cálculo de su pendiente al pie:
Por lo que la ecuación final de la recta, será:
Aproximando los tramos de subida por rectas, y el de bajada por una hipérbola, se puede reproducir bastante bien la respuesta de las células fotovoltaicas. En la figura que mostramos a continuación, los datos recabados aparecen en azul, y su reproducción con funciones calculadas en rojo:
Para representar estos puntos con LibreOffice Calc, proceder como se indica en el siguiente vídeo:
En 1º ESO, hemos trabajado especialmente con los dos primeros tramos (subida y mantenimiento), procurando que los alumnos busque las rectas que pueden aproximarlos teóricamente. En la subida, determinan la pendiente con dos puntos de esta región, y en el mantenimiento, saben que se trata de una recta horizontal. Ofrecemos como ejemplo, algunas gráficas de las alumnas Claudia y Andrea:
Descubridores
Lise Meitner (doctora en Físicas)
Otto Han (doctor en Química)
Primer reactor nuclear de la historia
Enrico Fermi
Proyecto Manhatan para el desarrollo de la primera bomba atómica
- James Franck.
- Józef (Joseph) Rotblat.
- Richard Feynman.
- John von Neumann.
- Enrico Fermi.
- Otto Robert Frisch.
- Robert Oppenheimer.
- Arthur Holly Compton, etc
Bomba H
Edward Teller
Posteriormente se comentan los riesgos para la salud de la ingente cantidad de residuos nucleares que se están generando, haciendo hincapié en el hecho de que los periodos de semidesintegración de estos materiales son de millones de años, y de que tomando las medidas oportunas, es posible autoabastecerse únicamente de energías renovables como la solar, sin tener que renunciar a nuestras necesidades energéticas. Puedes ver los resultados de esta reflexión, en la presentación que alumnos de 1º ESO y profesores vamos a representar en el IES Celestino Mutis durante la semana cultural, en una actuación por la tarde para padres, y para otros alumnos durante el período extraordinario del mes de junio:
Hemos querido acompañar la reflexión de este punto, con un proyecto de desarrollo y optimización escolar de fabricación y caracterización de células solares fotovoltaicas, utilizando materiales caseros y un procedimiento de trabajo manual sencillo y preciso, con el que hemos conseguido datos para trabajar los temas de Proporcionalidad, Porcentajes, Gráficas y Funciones:
Fabricación de células fotovoltaicas
Para construir una célula solar Grätzel:
U. Bach, D. Lupo, P. P Comte, J.E. Moser, F. Weissörtel, J. Salbeck, H. Spreitzer and M. Grätzel, “Solid-state dye-sensitized mesoporous TiO2 solar cells with high photon-to-electron conversion efficiencies”, Nature 398, 583 (1998).
Se necesitan:
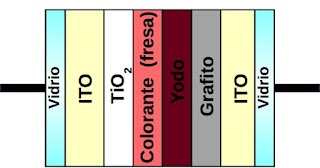
a) 2 placas de vidrio con semiconductor ITO.
b) Dióxido de titanio: , que puede conseguirse a partir del azúcar en polvo que venden en los supermercados, o comprarlo directamente en una droguería. Se utiliza mucho en la industria de alimentación, porque sirve para dar color blanco a los alimentos.
c) Ácido acético (vinagre).
d) 2 Fresas, frambuesas, moras, espinacas, o agua de col lombarda.
e) Yodo, o solución betadine de las farmacias.
f) Una mina gruesa de dureza 2B.
g) Una pinza.
Hacer una pasta con y unas gotas de vinagre, hasta formar una crema espesa y homogénea.
Disponer una capa de la pasta anterior sobre el lado conductor de una de las placas de vidrio. Para saber cuál es este, se apoyan cuidadosamente los dos contactos del polímetro sobre la placa. El pitido consiguiente del aparato, servirá como advertencia para saber que ese es el lado buscado. Y si no, será el otro:
La placa con se introduce en un horno a 150º durante 4 horas, con el objetivo de que la capa de este óxido quede bien adherida:
Aplastar las fresas o frambuesas en un mortero, y colocar una fina capa de este puré sobre el , con objeto de tintarlo. Lavar el exceso con etanol, utilizando una pipeta Pasteur, hasta eliminar todos los restos de pulpa y semillas de las frutas sobre la placa. Es mejor que no se incluyan semillas, y se deje secar el colorante:
Cuando así sea, se añaden unas gotas de betadine, y se deja reposar sobre la placa, mientas se extiende el grafito sobre la otra:
Tomar la otra placa de vidrio, y pintar el lado conductor con un lápiz para depositar una capa de grafito. También se puede exfoliar sobre la placa directamente con ayuda de unas tijeras:
Posteriormente solapar ambos fragmentos de vidrio, enfrentando las caras tratadas, y procurar que el conjunto permanezca unido con una o dos pinzas clip de tamaño proporcional al de las placas, de forma que se dejen dos extremos para colocar los cables de un polímetro:
El alumno debe tomar nota de la diferencia de potencial que hay entre las placas para distintos valores de la intensidad luminosa que incide sobre la placa solar: luz ambiente, y otras fuentes. Sin embargo, hemos comprobado que la respuesta no se estabiliza hasta pasadas unas horas.
Caracterización de células fotovoltaicas
Para estudiar la respuesta de las células ante la luz solar, hemos tomado vídeos de la tensión entre las placas frente a la radiación solar incidente. Dicha tensión se mide de dos formas:
1) Con banco óptico.
Con un banco óptico fabricado en coordinación con el departamento de Plástica: con dos cartones, un transportador y cinta adhesiva, se tiene una estructura como la de las siguientes figuras:
El banco óptico está bien orientado, cuando la sobra que proyecta el transportador es una línea.
Se puede enganchar a un trípode, si se ubica sobre un trozo de madera con un orificio para enganchar sobre el saliente del trípode.
Este montaje permite poner la célula frente al Sol, y abrir progresivamente de 10 en 10 grados, mientras se mide la tensión que esta desarrolla en consecuencia.
En todos los casos se observa que dicha tensión sube hasta alcanzar un máximo, y luego comienza a bajar, dando como resultado una gráfica con forma de parábola que se abre hacia abajo, y cuyo vértice se ubica para el ángulo de apertura asociado a la incidencia perpendicular sobre la célula fotovoltaica, que es cuando desarrolla su máximo rendimiento.
A continuación mostramos las parábolas logradas con tres de los colorantes estudiados:
Pudimos comprobar que los mejores resultados se consiguen para capas algo más gruesas de zumo de frambuesa (más cantidad), y más finas de grafito. En lugar de rayarlo sobre la oblea contraria, puede pintarse una capa muy fina, con un lápiz blando sobre la misma.
La célula se expone directamente desde la oscuridad, y se toma un vídeo de la tensión desarrollada en consecuencia hasta que llega a la saturación (valor máximo que es capaz de ofrecer). Posteriormente se cubre por completo, observando la evolución de la caída de tensión hasta que vuelve al valor de partida. Las gráficas tienen forma de escalón, con tres tramos claramente distintos:
Subida, mantenimiento y bajada.
Interpretación matemática
Los alumnos enseguida comprenden que las tres gráficas anteriores tienen tres tramos:
- Subida
- Mantenimiento
- Bajada
En la subida, la recta es inclinada, y su pendiente, número que da una idea de dicha inclinación, se calcula muy fácilmente, a partir de dos puntos:
Por ejemplo, considérense las rectas de las siguientes figuras, con el cálculo de su pendiente al pie:
Sin embargo, para sacar la ecuación completa de la recta, se necesita la ordenada en el origen, que es el número que aparece con la letra b, en la siguiente figura:
Para calcularlo, se sustituye un punto cualquiera en la ecuación de la recta. En el caso de la primera recta anterior, se tendría:
y=3x+2
La sección de mantenimiento, es una recta horizontal, y para ello, hay que saber que también tiene una ecuación especial. Mira la siguiente figura:
En 1º ESO, hemos trabajado especialmente con los dos primeros tramos (subida y mantenimiento), procurando que los alumnos busque las rectas que pueden aproximarlos teóricamente. En la subida, determinan la pendiente con dos puntos de esta región, y en el mantenimiento, saben que se trata de una recta horizontal. Ofrecemos como ejemplo, algunas gráficas de las alumnas Claudia y Andrea:
Estudio estadístico sobre el crecimiento de legumbres en condiciones extremas
Los alumnos han plantado unas 20 lentejas en tres botes que han sometido a distintas condiciones de cuidado:a) Con agua y luz.
b) Solo con luz.
c) Solo con agua (dentro de un armario).
Unas tres semanas después, comenzaron a realizar dos tipos de medidas en los tres botes:
1) Número de brotes.
2) Longitud de los brotes.
Para mostrar por ordenador los datos de este trabajo científico, es necesario tener instalado un paquete ofimático libre, que se puede descargar de:
https://es.libreoffice.org/
Se insiste al alumnado en la necesidad de no descargarlo de cualquier otra página, para evitar introducir virus y troyanos en su ordenador.
Una vez instalado, en este vídeo, pueden ver lo que las profesoras de Biología y Matemáticas piden analizar los datos de este trabajo:
Para aquellos que no puedan instalar el LibreOffice en sus equipos por cualquier motivo, saben que pueden descargar una versión portátil, que es un archivo que puede guardarse en cualquier disco duro, para trabajar desde cualquier ordenador. Se pueden descargar de:
https://es.libreoffice.org/descarga/versiones-portatiles/
Concursos de ecuaciones y problemas interdisciplinares
Para el campeonato de ecuaciones, debéis estar entrenados en dibujar ecuaciones en el ordenador. No hace falta que tengáis un dispositivo "Note taker". Solo un ratón lo más cómodo posible, y un lienzo pizarra "canvas", sobre el que podéis dibujar y escribir con dicho ratón.
Para ponerlo a pantalla completa, pulsad F11.
Para borrar lo escrito y comenzar de nuevo con una pantalla en blanco: F5.
Para salir del modo pantalla completa, también F11.
Podéis descargarlo del siguiente link:
Pizarra de ecuaciones
Permite diseñar cualquier cuerpo en el espacio, y determinar su área total y volumen.
Lo hemos aprovechado en el diseño de una catedral, con cálculos posteriores de volumen de piezas, aforo, presupuesto, etc.
Los detalles de este trabajo están en otra página del presente blog, a la que se accede a través del siguiente link:
Catedral con SketchUp
Contenidos trabajados: repaso general de casi toda la Geometría del curso e introducción a la Geometría del espacio de 2º ESO
1º) Construir un pentágono regular, lo más preciso posible, con el lado como único dato.
El alumno debe calcular primero el ángulo central de un pentágono regular: 72º.
Después, los otros dos ángulos internos de su triángulo central: 72º+X+X=180º, X=54º
Cuando los mida sobre los extremos de un segmento de longitud el lado del pentágono, conseguirá el centro y radio de la circunferencia circunscrita.
Una vez hecho correctamente uno de los pentágonos, se colocan cinco más, sobre cada uno de sus lados. Eso constituye la mitad del dodecaedro, y debe repetirse, por tanto, dos veces:
Posteriormente, se construyen los desarrollos de las pirámides, que constituyen los picos, dibujando un pentágono igual a los del dodecaedro, y prolongando dos de sus lados no contiguos, para lograr uno de los triángulos de la superficie lateral:
Este desarrollo se decora con explicaciones geométricas relacionadas con la pirámide, que podéis encontrar en el siguiente vídeo:
Una vez incluida la información pertinente, las pirámides se doblan de modo exhaustivo por sus caras laterales y aristas básicas, para formar las puntas de la estrella:
Mientras tanto, otro alumno del grupo deberá montar el núcleo de la estrella, que es el dodecaedro:
Una variante especialmente elegante, llegados a este punto, es incluir un cómic sobre los pentágonos del dodecaedro, incluyendo una historia relacionada con el hecho de que, para una misma altura, el volumen de la pirámide es la tercera parte que el de un prisma con idéntica base. Esta decoración se protegerá con film transparente, para pegar sobre las caras picos móviles, que puedan levantarse para leer el cómic, y observar la estructura del sólido platónico que hace de núcleo:
Diseño y cálculos de una catedral con SketchUp
Para una mejor observación de los cuerpos tridimensionales (poliedros y figuras de revolución) que se analizar con detalle por primera vez en 2º ESO, se puede utilizar un programa muy intuitivo que es el SketchUp.Permite diseñar cualquier cuerpo en el espacio, y determinar su área total y volumen.
Lo hemos aprovechado en el diseño de una catedral, con cálculos posteriores de volumen de piezas, aforo, presupuesto, etc.
Los detalles de este trabajo están en otra página del presente blog, a la que se accede a través del siguiente link:
Catedral con SketchUp
Trabajos de ampliación en período extraordinario
Estrella dodecaédrica
Construcción de un dodecaedro y doce pirámides pentagonales que constituirán sus picos.Contenidos trabajados: repaso general de casi toda la Geometría del curso e introducción a la Geometría del espacio de 2º ESO
1º) Construir un pentágono regular, lo más preciso posible, con el lado como único dato.
El alumno debe calcular primero el ángulo central de un pentágono regular: 72º.
Después, los otros dos ángulos internos de su triángulo central: 72º+X+X=180º, X=54º
Cuando los mida sobre los extremos de un segmento de longitud el lado del pentágono, conseguirá el centro y radio de la circunferencia circunscrita.
Una vez hecho correctamente uno de los pentágonos, se colocan cinco más, sobre cada uno de sus lados. Eso constituye la mitad del dodecaedro, y debe repetirse, por tanto, dos veces:
Posteriormente, se construyen los desarrollos de las pirámides, que constituyen los picos, dibujando un pentágono igual a los del dodecaedro, y prolongando dos de sus lados no contiguos, para lograr uno de los triángulos de la superficie lateral:
No hay comentarios:
Publicar un comentario